Tightly linked PMs are a series of two or more related PMs. Tightly linked PMs are not based on time (like the Scheduled PMs), but instead are based on how often an initial Scheduled PM is generated. In other words, tightly linked PM scheduling is based on the completion of other PMs, rather than scheduling based on the completion of the previous work order for the current PM. When a Tightly Linked PM is generated along with a Scheduled PM, both PMs will be associated with a single work order.
Regardless of the number of PMs in the program, the scheduling is based on a single Scheduled PM. The tightly linked PMs are generated by using the Affected PMs grid and indicating the # Between and # Remaining.

To demonstrate Tightly Linked PM Scheduling, we'll focus on when Work Orders are due. PMA represents the initial, Scheduled PM. PMB represents the tightly linked PM.
# Between:

# Between = 1
# Remaining

# Remaining = 1
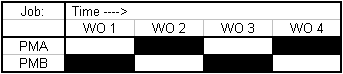
# Remaining = 0
Compound Scheduling
Using these settings, any number of sophisticated PM programs can be made. In this example, the initial Scheduled PM alternates with two jobs that alternate themselves. Remember, PMA is the initial Scheduled PM.

# Between = 3
# Remaining = 1
# Between = 3
# Remaining = 3
Note: You can start this compound scheduling program at any point in the cycle by setting the # Remaining to 0 and 2, 1 and 3, 2 and 0, or 3 and 1. The # Between always remains 3.